In BM, structured space starts with the idea of the spot unit, a spatial object which may contain two kinds of energy, M and L, shown by circles and arrows respectively (Fig. 2, upper right). Energy is quantized because M can only equal one or zero and L can only equal one or zero. These M and L types of energy are called 1-states or quanta. Quanta occur in quantized spatial cubes of size L which is the primary length constant in BM.
For any Theory of Everything (TOE) in physics you only need to define two things: (1) the system state -- what do we have? and (2) its time development -- how it changes over time. So let's do a walk-through of the basic postulates and equations of BM.
Full Quantization
With full quantization of energy, space and time, the next logical question is: what are the values in kg, meters and seconds of these quantized parameters? An important question since these values correspond to the basic units of measurement used in science.
System State
For energy quantization (expressed in kg), eqs. 1 is actually two equations seen in Fig. 2: M equals 0 or 1 and L equals 0 or 1. Max Planck wanted to quantize energy, but did not succeed. The closest he got was his famous Planck action constant h in units of Joules seconds. Now with full quantization, eqs. 1 finally completes the picture, expressing energy in kg, convertible to Joules with E = mc2.
Eq. 2 is the bit function which represents the states of the three M loci and three L loci in a spot (Fig. 2). The bit function replaces the wave function in antiquated, outdated, 20th century quantum mechanics (QM).
The bit function can include any number of spots. It just depends upon how big your computer is, how much computing power you have. Perhaps investigators may use computers at the US National Labs and CERN in Europe for studies using the Binary Mechanic Lab (BML) Simulator engine [6] to model physical processes. For example, one might model a single tick of the cesium 133 "clock" atom to see frame by frame exactly how it works. New BML technology offers both spatial and temporal resolution many orders of magnitude better than, say, electron microscopy and attosecond level measurements observed in experiments.
Next, a spatial frame Si, i = 1, 2, 3, in three dimensions is defined with integer coordinates for spot locations. Eq. 3 defines the even-odd parity of any position in this space and is zero or one for even or odd respectively. Eqs. 4 apply eq. 3 to define the X, Y and Z parities of any spot by its integer coordinate position in space S.
Next, the x, y and z dimensions in space S is a cyclic ordered set which exhibits chirality. Let I, J and K represent the three parities of each spot unit oriented along a particular x, y or z dimension of S (Fig. 2, lower left). Chirality maps X, Y and Z parities (eqs. 4) to I, J and K parities respectively (Fig. 3, lower).
With this information, eq. 5 defines the electric charge for a quanta in a M locus which can also be used to determine its color charge (Appendix A in [1]). This function is named sign(M) and raises -1 to the power of spot unit I parity, which equals +1 or -1. From simple algebra, if we raise any number to the zero power, it equals one and if we raise -1 to the power of 1, the result is -1.
Eq. 6 defines the sign(L) function raising -1 to the power of the K parity, providing the order of M and L loci in a spot unit or simply, its direction as +1 or -1. We just establish a convention that +1 is right or left and -1 is the other direction and we move along our jolly way.
We've now defined our system state. That wasn't too tough, was it? It is one half of what is needed for a Theory of Everything (TOE).
System State Results
Table 1 rows list the x, y and z spot units of the bit function B for each particle spot (columns) in three ways: (1) symbols (+, -, <, >), (2) signed L and M locus pairs and (3) signed pairs in complex format for reference for lovers of complex numbers.
Position in the spot cube alone determines elementary particle properties.
(1) electric charge Q is one third of the sum of the sign(Mi) values.
(2) handedness H is the product of the sign(Li) values.
(3) color charge is red, green, blue for the d quarks and none for the leptons.
(4) matter vs antimatter category [7]. Matter spots have two or three odd xyz coordinate parities.
This is a remarkable set of results from the simple equations for system state (Fig. 3). Three factors are said to be important in real estate: location, location and location. The same appears to apply to particle physics regarding spot position in the spot cube.
Time Evolution of System State
Time development describes how the bit function B changes over time.
1. The unconditional bit operation is a simple shifting of quanta in the L locus direction. Within spot units, the state (0 or 1) of the M locus shifts to the L locus in eq. 7. Eq. 8 says that the new state of the M locus equals the "carry bit" Lx from the prior spot unit.
2. The scaler bit operation requires the presence of an electrostatic potential labelled φ in eq. 9 defined by the state of locus MJ adjacent to its concurrent M quanta, as shown in Fig. 6, left. If the MJ locus state is one or true, an electrostatic potential exists at that location.
Each of the three forces in BM is defined as the product (or AND function) of three items: (1) a source 1-state quanta, (2) a potential in an adjacent locus and (3) a 0-state (empty) destination locus. If all three values are true, then the source quanta moves to the destination locus.
Note that a disassociation of potentials and motion occurs if the source and potential are true, but the destination is not empty. In other words, potentials may not result in quanta motion because a particular locus can only contain one quanta at a time. If it could contain more than one, then BM would not have really reduced things down to a fundamental level where a spatial cube locus can contain no more than one quanta.
3. The vector bit operation requires the presence of a magnetic potential labelled A equal to LK in eq. 12, which is one component of the magnetic vector A in the Lorentz force. LK is adjacent to its countercurrent M quanta, as shown in Fig. 6, right. If the LK is one or true, a magnetic potential exists at that location.
Eq. 13 defines the magnetic Lorentz force component as the product (or AND function) MLK. In Eq. 14 for vector force F, if MLK is one or true and the destination locus L is empty (1-L), then the M quanta moves to the L locus in its spot unit (eq. 7).
Is BM a field theory? Yes. All 1-state M loci are the electric field and all 1-state L loci are the magnetic field. Not all elemental volumes of space have these field potentials. Only those that have 1-state energy. Incidentally, the magnetic field may be the long sought after magnetic monopoles.
Hence, BM simplifies life for theoretical physicists because we don't need an infinite number of points in any arbitrary spatial volume, according to the obsolete theory that space and time are continuous and the miracles required by failed attempts to make that theory work. In contrast, all we need is our elemental volumes defined by the primary length constant L in BM. In addition, studies might focus on the total energy field, namely all M and L quanta.
Everything in the first three bit operations occur in one dimension so that when we are running our universe or running our computer simulation program, it does not matter which spatial dimension x, y or z we compute first because what occurs in these three bit operations is independent of the other dimensions. So we can do the x, y and z dimensions one at a time to get the new state of our world.
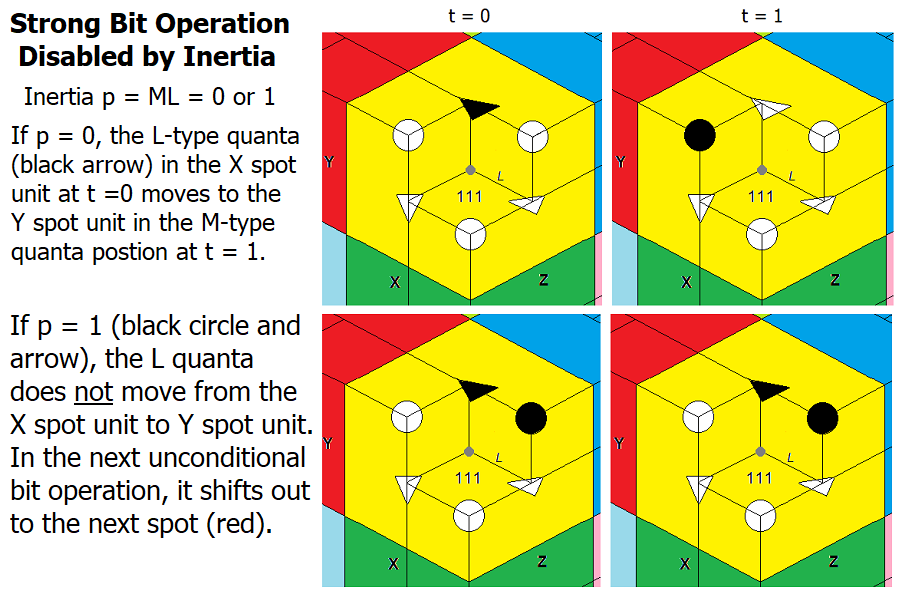
4. The strong bit operation is different, however. It deals with the transfer of quanta within a spot or intraspot. In strong force eq. 15, a source quanta Bi is a 1-state locus in a source spot unit. Its potential is a 0-state in the other locus in the source spot unit (1 - Bi*), which is a neutrino. As in the scalar and vector bit operations, a 0-state (empty) destination locus is required (1 - Bd) where d designates the destination spot unit within the spot.
In sum, a quanta moves from one spot unit to another within a spot if strong F is true. Considering the three spatial dimensions as a cyclic ordered set (chirality), the destination spot unit depends on the handedness of the elementary particle (spot) (Table 1). Eq. 16 defines the next n or previous p spot unit in a spot with reference to the source spot unit. Hence, subscript d in eq. 15 may be n or p. For left-handed particles such as the electron, i-to-n transfers move a quanta from x to y, y to z or z to x. For right-handed particles such as the matter d quarks (Table 1), the intraspot quanta transfer is i-to-p: x to z, y to x or z to y.
The strong potential 0-state loci, (1 - Bi*) in eq. 15, define a neutrino field which is the one's complement of the energy field described above as the sum of the electric and magnetic fields in eqs. 9 and 12 respectively.
Eq. 17 addresses the question of bit operations order. Our universe runs like a looping computer program. That is, its system state bit function B at t = 0 is altered by sequential application of the four bit operations which generates a new system state at t = 4. At present, the physically correct bit operations order is thought to be S (scalar), U (unconditional), V (vector) and F (strong). This is how simple a theory of everything can be.
The four bit operations do not commute. That is, their application in different orders produces different results [8]. Therefore, only one bit operations order can be physically correct.
Be Practical When Building a Universe
At this point, one may be asking, "When do we get to the hard part?". It seems that there is no hard part. In spite of continuing efforts by many physicists to sell lengthy and complex equations, the way the universe works may be summarized in rather simple binary logic equations (1 - 17) due to full quantization.
Theoretical physics needs to be very practical. One can't have 10 or 11 different dimensions (string theory). One can't have long complicated equations that nobody really understands, in which every little thing that wasn't taken into account before becomes another added term. History shows that just does not work. That is not parsimony, not Occam's razor and perhaps most of all, not practical.
Try to call up a supplier to order an infinite number of supercomputers that are infinitely small and that can sense things like objects and electric charges far away and sum up all that incoming information and then compute the value of that field instantaneously. The clerk at the order desk might respond, "Are you crazy? Is this a prank call? We don't have infinitely small computers. We don't do miracles here. Go talk to your priest, Rabbi or some other guru".
Mathematical Definition of Primary Forces
As shown in Fig. 8, the so-called "electromagnetic force" maps to two bit operations -- scalar and vector. The "strong force" maps to the strong bit operation.
The so-called "weak force and neutral weak force" involve the so-called plus or minus W bosons and the Z boson and map to the unconditional bit operation which alone produces these particle interactions [9]. The W and Z bosons have been identified as related to right-handed matter d quarks in BM. This view may be supported by experimental evidence when asking the right questions. The theories of the experimentalists as they gather their data may not matter. Maybe they are asking the wrong questions. One can look at their data and ask different questions, pose a different hypothesis and maybe come to a better conclusion.
Lastly, gravity is not a primary force. Actions of all four bit operations produce gravitational phenomena. Thus, quantum-gravitation unification is achieved in BM.
Moving from legacy physics in the 20th century (and for many people up to the present) to 21st century physics (Fig. 8, lower), the scalar, vector and strong force definitions each have three components: a source 1-state locus, an adjacent locus that has the potential for that force and a destination 0-state locus to receive an incoming quanta.
Discussion
If BM postulates defining system state and its time development are complete and correct then they are a comprehensive physical theory which suffices to represent fully any known physical system and its dynamics over time. Any exception would imply that the postulates are incomplete or incorrect to some extent.
Use of supposed particle interactions to define fundamental forces has failed to produce clear consistent results and lacks scientific merit.
Hopefully, this physics game walk-through has been fun and enjoyable.
5% Complete.
Do not turn off your brain until the update is complete.
References
[1] Keene, J. J. "Binary mechanics postulates" JBinMech November, 2020.
[2] Keene, J. J. "Physics standard model forensics" JBinMech May, 2015.
[3] Keene, J. J. "Quantization asymmetry" JBinMech May, 2016.
[4] Keene, J. J. "Binary mechanics FAQ" JBinMech August, 2018.
[5] Keene, J. J. "Fundamental physical constants doctrine" JBinMech October, 2020.
[6] Keene, J. J. "BML simulator interface" JBinMech March, 2016.
[7] Keene, J. J. "Matter-antimatter asymmetry mechanism" JBinMech October, 2014.
[8] Keene, J. J. "Bit operations order" JBinMech May, 2011.
[9] Keene, J. J. "Weak force boondoggle" JBinMech January, 2016.
© 2025 James J Keene